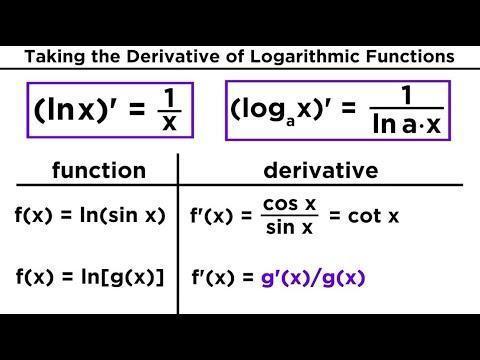
Differentiation of exponential and logarithmic functions| by vicky verma

We are aware that population generally grows but in some cases decay also. There are many other areas where growth and decay are continuous in nature. Examples from the fields of Economics, Agriculture and Business can be cited, where growth and decay are continuous. Let us consider an example of bacteria growth. If there are 10,00,000 bacteria at present and say they are doubled in number after 10 hours, we are interested in knowing as to after how much time these bacteria will be 30,00,000 in number and so on.

Answers to the growth problem does not come from addition (repeated or otherwise), or multiplication by a fixed number. In fact Mathematics has a tool known as exponential function that helps us to find growth and decay in such cases. Exponential function is inverse of logarithmic function. We shall also study about Rolle’s Theorem and Mean Value Theorems and their applications. In this lesson, we propose to work with this tool and find the rules governing their derivatives.

OBJECTIVES

After seen this video, you will be able to :

define and find the derivatives of exponential and logarithmic functions;

find the derivatives of functions expressed as a combination of algebraic, trigonometric, exponential and logarithmic functions; and

find second order derivative of a function.

state Rolle’s Theorem and Lagrange’s Mean Value Theorem; and

test the validity of the above theorems and apply them to solve problems.

EXPECTED BACKGROUND KNOWLEDGE

● Application of the following standard limits :

Definition of derivative and rules for finding derivatives of functions.

DERIVATIVE OF EXPONENTIAL FUNCTIONS

Working rule :

Solution :

CHECK YOUR PROGRESS 28.1

DERIVATIVE OF LOGARITHMIC FUNCTIONS

Working rule :

Part-1th

CHECK YOUR PROGRESS 28.2

DERIVATIVE OF LOGARITHMIC FUNCTION (CONTINUED)

CHECK YOUR PROGRESS 28.3

SECOND ORDER DERIVATIVES

In the previous lesson we found the derivatives of second order of trigonometric and inverse trigonometric functions by using the formulae for the derivatives of trigonometric and inverse trigonometric functions, various laws of derivatives, including chain rule, and power rule discussed earlier in lesson 21. In a similar manner, we will discuss second order derivative of exponential and logarithmic functions :

CHECK YOUR PROGRESS 28.4

DERIVATIVE OF PARAMETRIC FUNCTIONS

Sometimes x and y are two variables such that both are explicitly expressed in terms of a third variable, say t, i.e. if x = f(t) and y = g(t), then such functions are called parametric functions and the third variable is called the parameter.

In order to find the derivative of a function in parametric form, we use chain rule.